


Nächste Seite: Der Vergleich
Aufwärts: Gemeinsame In- und Outdegree
Vorherige Seite: Die unkorrelierte Verteilung
Inhalt
Im Gegensatz zu der vorangehenden Näherung (4.2) sagt das Modell von
Krapivsky et al. [8] eine korrelierte Form der gemeinsamen
Verteilung 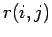 vorher (vgl. Abschnitt 2.3.4).
vorher (vgl. Abschnitt 2.3.4).
Für die Bestimmung der gemeinsamen Verteilung
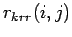 des Modells wird die
Rekursionsformel (2.19) benutzt
des Modells wird die
Rekursionsformel (2.19) benutzt
Darin sind 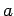 ,
,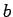 Konstanten. Aufgrund
der diskreten Natur dieser Verteilung läßt sich die Verteilung sehr
gut numerisch bestimmen. Mit dem
Exponenten der Indegree-Verteilung
Konstanten. Aufgrund
der diskreten Natur dieser Verteilung läßt sich die Verteilung sehr
gut numerisch bestimmen. Mit dem
Exponenten der Indegree-Verteilung 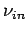 , dem Exponenten der Outdegree-Verteilung
, dem Exponenten der Outdegree-Verteilung 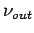 und
der Anzahl von Knoten
und
der Anzahl von Knoten 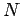 und Links
und Links 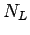 des Webcrawls können die
Parameter des Modells
des Webcrawls können die
Parameter des Modells 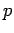 ,
, 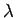 ,
, 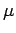 bestimmt werden. Aus
(2.22, 2.23, 2.16) und
bestimmt werden. Aus
(2.22, 2.23, 2.16) und 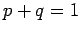 folgt durch einfache Umformung:
folgt durch einfache Umformung:
Bei diesem Modell gelten folgende Randbedingungen:
- Jeder Knoten entsteht mit einem Outlink, daher ist
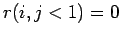 .
.
- Es existieren keine Knoten mit Indegree kleiner 0,
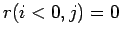 .
.
Mit diesen Bedingungen und (4.3) folgt
für den Ausgangspunkt der Rekursion
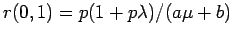 .
Die gemeinsame Verteilung
.
Die gemeinsame Verteilung
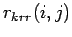 des Modells ist in Abbildung 4.4
dargestellt.
des Modells ist in Abbildung 4.4
dargestellt.
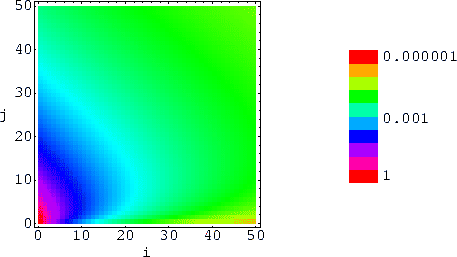
Abbildung:
Gemeinsame Verteilung
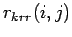 des Modells von Krapivsky
et al. mit den
Parametern
des Modells von Krapivsky
et al. mit den
Parametern
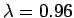 ,
, 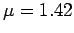 und
und 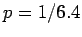 , die nach den Gleichungen
(4.4 - 4.6) aus den Daten des Webcrawls
bestimmt wurden.
Die Färbung gibt den Logarithmus der Wahrscheinlichkeit an, einen Knoten
mit Inlinks i und Outlinks j zu finden. Die Verteilung ist
auf
, die nach den Gleichungen
(4.4 - 4.6) aus den Daten des Webcrawls
bestimmt wurden.
Die Färbung gibt den Logarithmus der Wahrscheinlichkeit an, einen Knoten
mit Inlinks i und Outlinks j zu finden. Die Verteilung ist
auf
 normiert.
normiert.
 |



Nächste Seite: Der Vergleich
Aufwärts: Gemeinsame In- und Outdegree
Vorherige Seite: Die unkorrelierte Verteilung
Inhalt
Autor:Lutz-Ingo Mielsch
