


Nächste Seite: Vorhersage des Modells von
Aufwärts: Gemeinsame In- und Outdegree
Vorherige Seite: Die Verteilung des Webcrawl
Inhalt
In einer ersten Näherung werden Korrelationen
zwischen Indegree und Outdegree der Knoten vernachlässigt. Die gemeinsame
Verteilung 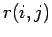 kann daher aus den einzelnen Verteilungen
kann daher aus den einzelnen Verteilungen 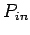 und
und
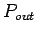 konstruiert werden
konstruiert werden
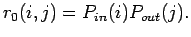 |
(4.2) |
Mit
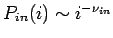 und
und
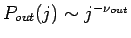 kann für
kann für 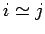 bereits abgeschätzt werden, daß
bereits abgeschätzt werden, daß
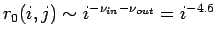 ist. Damit entspricht die Wahrscheinlichkeit
einen Knoten bei
ist. Damit entspricht die Wahrscheinlichkeit
einen Knoten bei 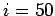 zu finden, etwa
zu finden, etwa 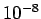 . Bei einer Netzwerkgröße
des Webcrawl von
. Bei einer Netzwerkgröße
des Webcrawl von
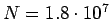 Knoten, werden einzelne Knoten im Mittel erst
ab einer Wahrscheinlichkeit von
Knoten, werden einzelne Knoten im Mittel erst
ab einer Wahrscheinlichkeit von 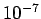 erwartet.
Die Größe des belegten Wertebereiches der Verteilung
erwartet.
Die Größe des belegten Wertebereiches der Verteilung
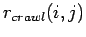 ist
bereits ein erstes Indiz für eine Korrelation zwischen In- und Outdegree
der Knoten.
ist
bereits ein erstes Indiz für eine Korrelation zwischen In- und Outdegree
der Knoten.
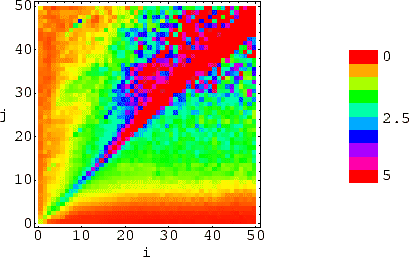
Abbildung:
Gemeinsame Verteilung des Webcrawls
normiert mit der unkorrelierten Verteilung
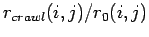 .
Die Färbung gibt die Abweichung der Wahrscheinlichkeiten für einen Knoten
mit
.
Die Färbung gibt die Abweichung der Wahrscheinlichkeiten für einen Knoten
mit 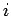 Inlinks und
Inlinks und 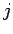 Outlinks an (lineare Farbskala).
Outlinks an (lineare Farbskala).
 |
Für diese Näherung werden die gemessenen Verteilungen
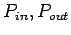 (vgl.
Abb. 3.4, Abb. 3.5) verwendet, um den
typischen, anfänglich exponentiellen Verlauf der Outdegree-Verteilung zu beachten.
In Abbildung 4.2 ist die Verteilung des Webcrawls normiert mit
der Näherung
(vgl.
Abb. 3.4, Abb. 3.5) verwendet, um den
typischen, anfänglich exponentiellen Verlauf der Outdegree-Verteilung zu beachten.
In Abbildung 4.2 ist die Verteilung des Webcrawls normiert mit
der Näherung
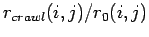 dargestellt. Unterschiede manifestieren
sich daher als Abweichungen von Eins.
dargestellt. Unterschiede manifestieren
sich daher als Abweichungen von Eins.
Besonders auffällig ist die deutlich hervortretende Diagonale. Die
Ursachen hierfür werden in Abschnitt 4.5 diskutiert. An dieser
Stelle interessiert zunächst, ob die Potenzgesetze korrekt wiedergegeben
werden. Daher ist der Bereich der Verteilung außerhalb des Einflusses der Diagonalen
interessant. Um diesen Bereich genauer darzustellen
ist der Wertebereich für die Färbung auf 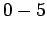 eingeschränkt. Werte
jenseits von 5 erhalten daher die Färbung von 5.
eingeschränkt. Werte
jenseits von 5 erhalten daher die Färbung von 5.
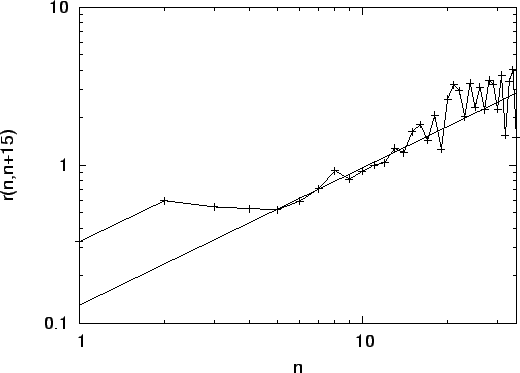
Abbildung:
Diagonaler Schnitt durch die Abbildung 4.2
ausgehend von 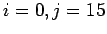 , parallel zur hervortretenden
Diagonale. Es ist ein deutlich abweichender Verlauf zwischen der
unkorrelierten Verteilung und der Verteilung des Webcrawls zu sehen. Die
angelegte Gerade entspricht einem Exponenten von
, parallel zur hervortretenden
Diagonale. Es ist ein deutlich abweichender Verlauf zwischen der
unkorrelierten Verteilung und der Verteilung des Webcrawls zu sehen. Die
angelegte Gerade entspricht einem Exponenten von 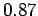 .
.
 |
Mit zunehmenden 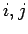 erkennt man eine deutlich höhere Präsenz von Knoten
im Webcrawl als in der Näherung (4.2). In Abbildung 4.3
ist ein diagonaler Schnitt durch die normierte Verteilung aus Abbildung 4.2
dargestellt, um den Verlauf klarer zu zeigen. Der Schnitt geht
von
erkennt man eine deutlich höhere Präsenz von Knoten
im Webcrawl als in der Näherung (4.2). In Abbildung 4.3
ist ein diagonaler Schnitt durch die normierte Verteilung aus Abbildung 4.2
dargestellt, um den Verlauf klarer zu zeigen. Der Schnitt geht
von 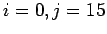 mit einer Steigung von 1 aus, um einerseits möglichst außerhalb des Einflußes
der Diagonalen zu bleiben, andererseits möglichst viele Datenpunkte zu
erhalten.
mit einer Steigung von 1 aus, um einerseits möglichst außerhalb des Einflußes
der Diagonalen zu bleiben, andererseits möglichst viele Datenpunkte zu
erhalten. 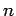 bezeichnet den Abstand von Ursprung des Schnittes.
Damit Abweichungen von dem Potenzgesetz (4.2)
deutlicher werden, sind die Daten doppeltlogarithmisch aufgetragen. Bei
einer qualitativen Übereinstimmung des Verlaufs der gemessenen Verteilung und der
Näherung wird in diesem Schnitt ein paralleler Verlauf zur X-Achse erwartet.
Im Bereich bis
bezeichnet den Abstand von Ursprung des Schnittes.
Damit Abweichungen von dem Potenzgesetz (4.2)
deutlicher werden, sind die Daten doppeltlogarithmisch aufgetragen. Bei
einer qualitativen Übereinstimmung des Verlaufs der gemessenen Verteilung und der
Näherung wird in diesem Schnitt ein paralleler Verlauf zur X-Achse erwartet.
Im Bereich bis 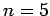 ist der Verlauf relativ gut wiedergegeben. Zu höheren
Degrees zeigt sich jedoch eine deutliche Abweichung. Die angelegte Gerade entspricht einem
Exponenten von
ist der Verlauf relativ gut wiedergegeben. Zu höheren
Degrees zeigt sich jedoch eine deutliche Abweichung. Die angelegte Gerade entspricht einem
Exponenten von 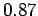 . Weitere Schnitte parallel zur X-Achse und Y-Achse
zeigen ähnliche Abweichungen.
. Weitere Schnitte parallel zur X-Achse und Y-Achse
zeigen ähnliche Abweichungen.
Der Vergleich zeigt, daß die einzelnen Verteilungen der In- und Out-Degrees
korreliert sind.



Nächste Seite: Vorhersage des Modells von
Aufwärts: Gemeinsame In- und Outdegree
Vorherige Seite: Die Verteilung des Webcrawl
Inhalt
Autor:Lutz-Ingo Mielsch

