

Nächste Seite: Vermessung des deutschen World-Wide-Web
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Das Modell von Bornholdt
Inhalt
Das Modell von Krapivsky, Rodgers und Redner
Bereits bei dem Modell von Dorogovtsev et al. kündigte sich ein
nächster Schritt der Modellierung an: ein Modell für gerichtete Netzwerke.
Einige der größten untersuchten skalenfreien Netzwerke sind
gerichteter Natur, wie z.B. das Netzwerk aus Zitierungen in
wissenschaftlichen Veröffentlichungen oder das WWW. Die Topologie solcher
Netzwerke läßt sich jedoch nicht nur mit einer Degree-Verteilung
beschreiben, sondern die Unterscheidung nach Indegree-Verteilung 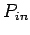 und Outdegree-Verteilung
und Outdegree-Verteilung 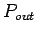 gibt einen genaueren Einblick in deren
Struktur. Diese Verteilungen sind für gerichtete Netzwerke bestimmt worden
und eine Reihe dieser Netze zeigten jeweils ein Potenzgesetz mit
unterschiedlichen Exponenten (vgl. Tab. 1.1).
gibt einen genaueren Einblick in deren
Struktur. Diese Verteilungen sind für gerichtete Netzwerke bestimmt worden
und eine Reihe dieser Netze zeigten jeweils ein Potenzgesetz mit
unterschiedlichen Exponenten (vgl. Tab. 1.1).
Das Modell von Krapivsky, Rodgers und Redner [8] ermöglicht
es, Netzwerke zu erzeugen, deren Indegree- und Outdegree-Verteilung
jeweils skalenfrei sind, mit den Exponenten 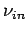 und
und
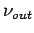 .
Die Wachstumsdynamik läßt sich, je Zeitschritt, durch zwei
mögliche Prozesse beschreiben:
.
Die Wachstumsdynamik läßt sich, je Zeitschritt, durch zwei
mögliche Prozesse beschreiben:
- (i)
- Knoten-Wachstum: Mit der Wahrscheinlichkeit
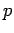 wird dem
Netzwerk ein neuer Knoten hinzugefügt und mit einem älteren Knoten
verbunden. Die Wahrscheinlichkeit eines bestehenden Knotens als Ziel
gewählt zu werden, hängt von dessen Indegree ab.
wird dem
Netzwerk ein neuer Knoten hinzugefügt und mit einem älteren Knoten
verbunden. Die Wahrscheinlichkeit eines bestehenden Knotens als Ziel
gewählt zu werden, hängt von dessen Indegree ab.
- (ii)
- Link-Wachstum: Mit der Wahrscheinlichkeit
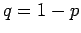 wird eine
Verbindung zwischen zwei bereits bestehenden Knoten geknüpft. Die Wahl
des Urspungsknotens hängt von dessen Outdegree ab und die Wahl des
Zielknotens von dessen Indegree.
wird eine
Verbindung zwischen zwei bereits bestehenden Knoten geknüpft. Die Wahl
des Urspungsknotens hängt von dessen Outdegree ab und die Wahl des
Zielknotens von dessen Indegree.
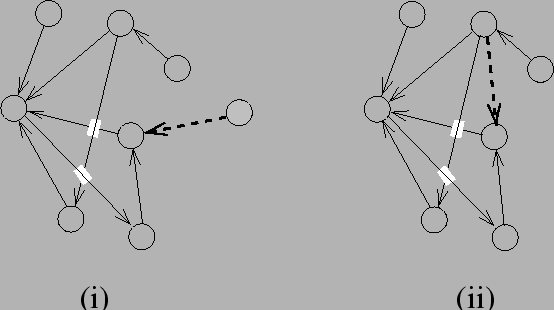
Die Abbildung 2.3 illustriert die beiden Wachstumsprozesse.
Abbildung:
Die Wachstumsprozesse im Krapivsky et al. Modell:
(i) Hinzufügen eines neuen Knoten mit direktem Anknüpfen an einen
bestehenden Knoten. (ii) Erzeugen einer Verbindung. Aus Krapivsky et al. [8]
 |
Seien 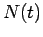 die Anzahl der Knoten,
die Anzahl der Knoten, 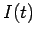 die gesamte Anzahl der Inlinks und
die gesamte Anzahl der Inlinks und
 die gesamte Anzahl Outlinks in einem Netzwerk zum Zeitpunkt
die gesamte Anzahl Outlinks in einem Netzwerk zum Zeitpunkt
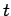 . Entsprechend den
beiden Wachstumsregeln des Modells entwickeln sich die Gesamtanzahlen:
. Entsprechend den
beiden Wachstumsregeln des Modells entwickeln sich die Gesamtanzahlen:
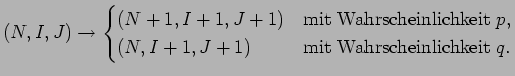 |
(2.14) |
Mit der Wahrscheinlichkeit 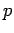 wird ein neuer Knoten hinzugefügt und mit einem
gerichteten Link ans Netzwerk angebunden,
folglich nehmen die Knotenanzahl und beide
Gesamtkonnektivitäten jeweils um eins zu. Mit der Wahrscheinlichkeit
wird ein neuer Knoten hinzugefügt und mit einem
gerichteten Link ans Netzwerk angebunden,
folglich nehmen die Knotenanzahl und beide
Gesamtkonnektivitäten jeweils um eins zu. Mit der Wahrscheinlichkeit 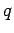 wird nur ein neuer Link hinzugefügt, so daß
wird nur ein neuer Link hinzugefügt, so daß 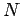 konstant bleibt.
Dementsprechend entwickeln sich die Werte mit der Zeit nach:
konstant bleibt.
Dementsprechend entwickeln sich die Werte mit der Zeit nach:
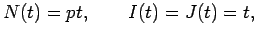 |
(2.15) |
daraus lassen sich unmittelbar der mittlere In- und Outdegree bestimmen,
 |
(2.16) |
Beide sind zeitunabhängig und gleich 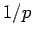 . Um die gemeinsame Verteilung
zu bestimmen müssen noch die Auswahlmechanismen spezifiziert werden.
. Um die gemeinsame Verteilung
zu bestimmen müssen noch die Auswahlmechanismen spezifiziert werden.
Krapivsky, Leyvraz und Redner [32] zeigten, daß skalenfreie
Verteilungen nur für lineare Raten zu erwarten sind.
Die Raten werden analog zum Modell von Dorogovtsev zum
Wachstum skalenfreier Netze gewählt.
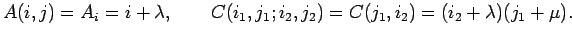 |
(2.17) |
Die Parameter 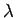 und
und 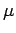 müssen den Bedingungen
müssen den Bedingungen
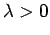 und
und
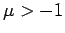 genügen, damit die Raten für alle möglichen Werte
des Indegree
genügen, damit die Raten für alle möglichen Werte
des Indegree 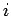 und des Outdegree
und des Outdegree 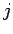 positiv sind,
positiv sind, 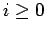 und
und 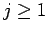 . Diese
Raten entsprechen einem ``Preferential Attachment'' bzw. ``Preferential
Update'' von Verbindungen nach dem bekannten Mechanismus früherer Modelle, aus
einer anfänglichen Attraktivität
. Diese
Raten entsprechen einem ``Preferential Attachment'' bzw. ``Preferential
Update'' von Verbindungen nach dem bekannten Mechanismus früherer Modelle, aus
einer anfänglichen Attraktivität 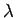 ,
, 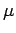 und einer linearen
Abhängigkeit vom In- bzw. Outdegree. Diese Form der Raten wird linear-bilineare Form genannt.
und einer linearen
Abhängigkeit vom In- bzw. Outdegree. Diese Form der Raten wird linear-bilineare Form genannt.
Mit dem Wachstum des Netzwerks entwickelt sich die gemeinsame
Verteilung 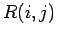 , definert als die relative Anzahl von Knoten mit Indegree
, definert als die relative Anzahl von Knoten mit Indegree
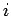 und Outdegree
und Outdegree 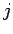 im Netzwerk. Nach Krapivsky et al. kann die
Form der Verteilung mit folgendem Differentialgleichungsansatz bestimmt
werden.
im Netzwerk. Nach Krapivsky et al. kann die
Form der Verteilung mit folgendem Differentialgleichungsansatz bestimmt
werden.
Der erste Summand beinhaltet die Änderung des Indegree der Zielknoten.
Diese Änderung tritt sowohl beim Knoten-Wachstum, als auch beim Link-Wachstum auf
(Wahrscheinlichkeit 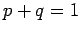 ). Beide Prozesse erzeugen einen neuen Link,
dessen Ziel via ``Preferential Attachment'' gewählt wird. Die Anzahl der
Knoten mit Indegree
). Beide Prozesse erzeugen einen neuen Link,
dessen Ziel via ``Preferential Attachment'' gewählt wird. Die Anzahl der
Knoten mit Indegree 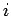 nimmt um eins zu, wenn ein Knoten mit Indegree
nimmt um eins zu, wenn ein Knoten mit Indegree
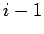 diesen Inlink erhält. Verringert sich um einen Knoten, wenn dieser Inlink
einem Knoten zugefügt wird, dessen Indegree bereits
diesen Inlink erhält. Verringert sich um einen Knoten, wenn dieser Inlink
einem Knoten zugefügt wird, dessen Indegree bereits 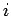 ist. Der zweite
Summand bestimmt die Änderungen im Outdegree der Quellknoten. Hier wirkt
nur das Link-Wachstum (Wahrscheinlichkeit
ist. Der zweite
Summand bestimmt die Änderungen im Outdegree der Quellknoten. Hier wirkt
nur das Link-Wachstum (Wahrscheinlichkeit 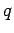 ), da nur dieser Prozeß eine
Änderung im Outdegree bestehender Knoten bewirkt. Bei dem Hinzufügen eines
Links wird der Quellknoten via ``Preferential Update'' gewählt. Der dritte
Summand repräsentiert das Auftreten neuer Knoten, die nur
einen Outlink und keinen Inlink besitzen (Wahrscheinlichkeit
), da nur dieser Prozeß eine
Änderung im Outdegree bestehender Knoten bewirkt. Bei dem Hinzufügen eines
Links wird der Quellknoten via ``Preferential Update'' gewählt. Der dritte
Summand repräsentiert das Auftreten neuer Knoten, die nur
einen Outlink und keinen Inlink besitzen (Wahrscheinlichkeit 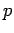 ).
).
Krapivsky et al. zeigten durch Betrachtungen der Lösungen des
Gleichungssystems (2.18), daß sich  linear mit der Zeit
entwickelt. Es kann daher
linear mit der Zeit
entwickelt. Es kann daher  durch die stationäre Form
durch die stationäre Form
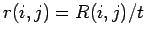 substituiert werden. Mit
substituiert werden. Mit 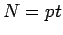 , und
, und 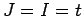 und
folgenden Ersetzungen
und
folgenden Ersetzungen
ergibt sich eine Rekursionsformel für 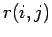
Aus der gemeinsamen Verteilung 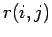 lassen sich die
Indegree- und Outdegree-Verteilung durch die Summen
lassen sich die
Indegree- und Outdegree-Verteilung durch die Summen
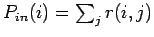 und
und
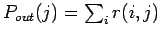 bestimmen.
Krapivsky, Rodgers und Redner zeigten, daß sich aus (2.19) die
Verteilungen
bestimmen.
Krapivsky, Rodgers und Redner zeigten, daß sich aus (2.19) die
Verteilungen
ableiten lassen. Die Exponenten bestimmen sich aus den Parametern
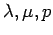 des Modells nach
des Modells nach
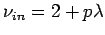 |
|
|
(2.22) |
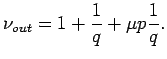 |
|
|
(2.23) |
Dieses Modell ist in der Lage die
gegenwärtig bestimmten Degreeverteilungen von realen, skalenfreien Netzwerken
wiederzugeben. Darüber hinaus bietet es die Möglichkeit, Aussagen über die
gemeinsame Verteilung 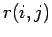 der Knoten eines Netzwerks in Abhängigkeit
von deren Indegree und Outdegree zu treffen.
der Knoten eines Netzwerks in Abhängigkeit
von deren Indegree und Outdegree zu treffen.



Nächste Seite: Vermessung des deutschen World-Wide-Web
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Das Modell von Bornholdt
Inhalt
Autor:Lutz-Ingo Mielsch