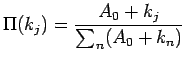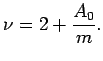


Nächste Seite: Das Modell von Bornholdt
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Das Modell von Barabási
Inhalt
Dorogovtsev et al. erweiterteten das BA-Modell, um dessen Schwächen zu
beheben. In diesem Modell wird aus eher praktischen Gründen ein
gerichtetes Netzwerk betrachtet. Das Modell beschränkt sich in allen
Untersuchungen auf die eingehenden Verbindungen eines Knotens,
um die Verbindungen losgelöst von deren Quelle betrachten zu können. Das
erlaubt einerseits die Existenz von externen Verbindungen, d.h.
Verbindungen von außerhalb des Netzes zu Knoten im Netzwerk. Andererseits
sind mehrfache identische Verbindungen möglich und lassen folgende
Anfangsbedingungen für das Modell zu.
Das Modell beginnt zum Zeitpunkt 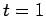 mit einem Knoten mit Indegree
mit einem Knoten mit Indegree
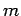 . In jedem Zeitschritt werden ein neuer Knoten und
. In jedem Zeitschritt werden ein neuer Knoten und 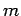 Inlinks
mit willkürlichem Ursprung zu den Knoten
des Netzwerk hinzugefügt. Diese Inlinks werden in Abhängigkeit von der
Attraktivität
Inlinks
mit willkürlichem Ursprung zu den Knoten
des Netzwerk hinzugefügt. Diese Inlinks werden in Abhängigkeit von der
Attraktivität 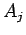 der einzelnen Knoten
der einzelnen Knoten 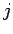 im Netzwerk verteilt. Die Attraktivität
im Netzwerk verteilt. Die Attraktivität
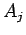 der Knoten
der Knoten
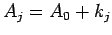 |
(2.9) |
setzt sich zum einen aus einer konstanten anfänglichen Attraktivität 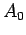 der Knoten und deren (In-)Degree
der Knoten und deren (In-)Degree 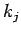 zusammen. Dementsprechend startet jeder
Knoten mit der Attraktivität
zusammen. Dementsprechend startet jeder
Knoten mit der Attraktivität 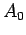 und wächst dann mit
und wächst dann mit 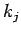 . Der Fall
. Der Fall
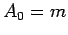 entspricht dem BA-Modell. Das Modell besteht zum Zeitpunkt
entspricht dem BA-Modell. Das Modell besteht zum Zeitpunkt 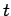 aus
aus
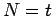 Knoten und
Knoten und 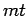 Verbindungen. Die Gesamtattraktivität der Knoten im
Netzwerk beträgt
Verbindungen. Die Gesamtattraktivität der Knoten im
Netzwerk beträgt
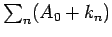 , wobei
, wobei 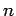 über alle Knoten in
Netzwerk summiert. Damit ist die Wahrscheinlichkeit, daß ein Knoten
über alle Knoten in
Netzwerk summiert. Damit ist die Wahrscheinlichkeit, daß ein Knoten 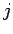 einen Inlink erhält
einen Inlink erhält
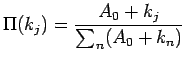 |
(2.10) |
Für dieses Modell läßt sich die Wachstumsdynamik folgendermaßen
zusammenfassen:
Die lange Herleitung [7] soll hier nicht wiedergeben werden, sondern
nur die wesentliche Eigenschaft des Modells, daß der Exponent der
Degree-Verteilung
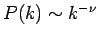 durch die beiden Parameter des
Modells,
durch die beiden Parameter des
Modells, 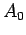 und
und 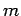 , Werte zwischen
, Werte zwischen 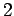 und
und 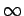 annehmen kann.
annehmen kann.
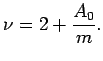 |
(2.11) |
Die Erweiterung des BA-Modells um eine Anfangsattraktivität von Knoten
stellt einen wichtigen Schritt auf dem Weg zu besseren Modellen realer
skalenfreier Netzwerke dar.
Ein Nachteil dieses Modells ist, daß die initiale Attraktivität von Knoten 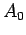 experimentell nicht zugänglich ist.
experimentell nicht zugänglich ist.



Nächste Seite: Das Modell von Bornholdt
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Das Modell von Barabási
Inhalt
Autor:Lutz-Ingo Mielsch