


Nächste Seite: Das Modell von Dorogovtsev,
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Skalenfreie Netzwerke
Inhalt
Die Modelle von Erdös und Renyi [9] sowie von Watts und
Strogatz [10] vernachlässigen zwei generische Eigenschaften von
vielen realen Netzwerken. Erstens gehen beide von einer konstanten Knotenanzahl
 aus, obwohl die meisten Netzwerke durch kontinuierliches Hinzufügen
neuer Knoten wachsen. Beispielsweise werden im Netzwerk der
wissenschaftlichen Zitierungen ständig neue Publikationen mit neuen
Referenzen hinzugefügt und das WWW wächst gegenwärtig durch das Hinzufügen von
Seiten exponentiell mit der Zeit [26]. Zweitens nehmen die
Modelle die Wahrscheinlichkeit, daß zwei Knoten miteinander verbunden sind,
als zufällig und gleich wahrscheinlich an. Die Dynamik der meisten realen Netze
zeigen jedoch einen Effekt, den man heute als ``Preferential Linking''
bezeichnet. So neigen zum Beispiel Autoren von wissenschaftlichen
Publikationen dazu, eher bereits populäre Arbeiten zu zitieren, welche
bereits einen hohen Degree besitzen. Ebenso tendieren Autoren von
Seiten im WWW dazu, Links auf Seiten von breitem Interesse zu legen, wie
Suchmaschinen, Zeitungen, Onlineportale, Onlineauktionshäuser, etc.
Diese Beispiele legen die Vermutung nahe, daß Verbindungen nicht
zufällig geknüpft werden, sondern Knoten mit einem bereits höheren
Degree auch eine höhere Wahrscheinlichkeit haben, weitere
Verbindungen von neuen Knoten zu bekommen.
aus, obwohl die meisten Netzwerke durch kontinuierliches Hinzufügen
neuer Knoten wachsen. Beispielsweise werden im Netzwerk der
wissenschaftlichen Zitierungen ständig neue Publikationen mit neuen
Referenzen hinzugefügt und das WWW wächst gegenwärtig durch das Hinzufügen von
Seiten exponentiell mit der Zeit [26]. Zweitens nehmen die
Modelle die Wahrscheinlichkeit, daß zwei Knoten miteinander verbunden sind,
als zufällig und gleich wahrscheinlich an. Die Dynamik der meisten realen Netze
zeigen jedoch einen Effekt, den man heute als ``Preferential Linking''
bezeichnet. So neigen zum Beispiel Autoren von wissenschaftlichen
Publikationen dazu, eher bereits populäre Arbeiten zu zitieren, welche
bereits einen hohen Degree besitzen. Ebenso tendieren Autoren von
Seiten im WWW dazu, Links auf Seiten von breitem Interesse zu legen, wie
Suchmaschinen, Zeitungen, Onlineportale, Onlineauktionshäuser, etc.
Diese Beispiele legen die Vermutung nahe, daß Verbindungen nicht
zufällig geknüpft werden, sondern Knoten mit einem bereits höheren
Degree auch eine höhere Wahrscheinlichkeit haben, weitere
Verbindungen von neuen Knoten zu bekommen.
Bei dem Modell von Barabási und Albert
[5,27] (BA-Modell) wurde nicht versucht die
Topologie eines Netzes direkt nachzubilden, sondern Regeln für das Wachstum
formuliert: Zu einem Zeitpunkt 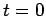 wird mit einer kleinen Anzahl von
Knoten
wird mit einer kleinen Anzahl von
Knoten 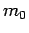 begonnen. In jedem weiterem Zeitschritt
begonnen. In jedem weiterem Zeitschritt 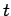 wird ein neuer
Knoten hinzugefügt und mit
wird ein neuer
Knoten hinzugefügt und mit
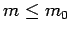 bereits bestehenden Knoten
verbunden. Die Auswahl der Knoten findet dabei nicht zufällig statt,
sondern in Abhängigkeit von dessen jeweiligem Degree
bereits bestehenden Knoten
verbunden. Die Auswahl der Knoten findet dabei nicht zufällig statt,
sondern in Abhängigkeit von dessen jeweiligem Degree 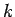 . Die
Wahrscheinlichkeit
. Die
Wahrscheinlichkeit 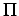 , einen Link an einen Knoten
, einen Link an einen Knoten 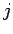 zu binden, hängt
linear von
zu binden, hängt
linear von 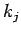 ab
ab
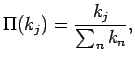 |
(2.7) |
wobei 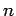 über das gesamte Netzwerk summiert, den neuen Knoten ausgenommen.
Aufgrund der Abhängigkeit zwischen der Wahrscheinlichkeit einen Link zu
bekommen und der Anzahl Links, die ein Knoten schon hat, spricht man von
``Preferential Attachment''. Ein Knoten mit vielen Links hat eine größere
Chance, weitere Links zu bekommen.
über das gesamte Netzwerk summiert, den neuen Knoten ausgenommen.
Aufgrund der Abhängigkeit zwischen der Wahrscheinlichkeit einen Link zu
bekommen und der Anzahl Links, die ein Knoten schon hat, spricht man von
``Preferential Attachment''. Ein Knoten mit vielen Links hat eine größere
Chance, weitere Links zu bekommen.
Die Wachstumsdynamik kann folgendermaßen zusammengefaßt werden:
Dieser Algorithmus erzeugt nach 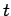 Zeitschritten ein Netzwerk mit
Zeitschritten ein Netzwerk mit
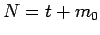 Knoten und
Knoten und 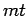 Verbindungen. Das Netzwerk entwickelt sich mit
Verbindungen. Das Netzwerk entwickelt sich mit
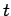 in einen stationären Zustand mit konstanter Degree-Verteilung nach einem
Potenzgesetz
in einen stationären Zustand mit konstanter Degree-Verteilung nach einem
Potenzgesetz
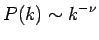 |
(2.8) |
Durch Untersuchung weiterer Modelle
zeigten Barabási und Albert, daß die beiden Eigenschaften Wachstum
und Preferential Attachment nötig sind, um diese skalenfreie Verteilungsform zu
erklären.
Ohne Preferential Attachment
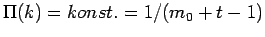 entspricht dieses Modell einem wachsenden Zufallsgraphen. Diese Graphen
haben jedoch eine exponentielle Degree-Verteilung
entspricht dieses Modell einem wachsenden Zufallsgraphen. Diese Graphen
haben jedoch eine exponentielle Degree-Verteilung
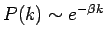 .
In einem Modell ohne Wachstum, aber mit Preferential
Attachment, nimmt
.
In einem Modell ohne Wachstum, aber mit Preferential
Attachment, nimmt 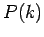 keinen stationären Zustand an, da die
Knotenanzahl
keinen stationären Zustand an, da die
Knotenanzahl 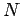 konstant bleibt, jedoch kontinuierlich neue Verbindungen
geknüpft werden. Nach der Zeit
konstant bleibt, jedoch kontinuierlich neue Verbindungen
geknüpft werden. Nach der Zeit
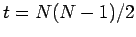 ist das Netzwerk vollständig
verbunden.
ist das Netzwerk vollständig
verbunden.
Obwohl die lineare Form des ``Preferential Attachments''
(2.7) nur einen speziellen
Fall darstellt, haben Untersuchungen an realen skalenfreien Netzen bisher nur diese
Form gefunden [28,29,30]. Eriksen und Hörnquist
[31] zeigten später, daß wachsende Netzwerke nur
für die lineare Form des ``Preferential Attachments'' eine Verteilung 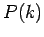 nach einem
Potenzgesetz haben.
nach einem
Potenzgesetz haben.
Die ersten Versuche mit dem BA-Modell führten Barabási und Albert
numerisch durch. Später sind verschiedene analytische Lösungen
vorgestellt worden. Barabási, Albert und Jeong [27]
stellten einen Kontinuumsansatz vor, Dorogovtsev, Mendes, Samukhin
[7] stellten einen Ansatz mit einer erzeugenden Funktion
vor, und Krapivsky, Redner, Leyvraz einen Differentialgleichungsansatz
[32]. Alle Ansätze bestätigen im Ergebnis die Verteilungsform
(2.8) mit 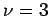 .
.
Dieses einfache Modell legt den Grundstein für das Verständnis der
generischen Mechanismen, die für die Wachstumsdynamik eines Netzes mit
skalenfreier Potenzgesetz-Verteilung notwendig sind.
Dennoch hat dieses Modell eine entscheidene Schwäche. Der Exponent der
Degree-Verteilung ist konstant 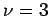 . Viele reale Netze zeigen zwar
ein skalenfreies Verhalten, aber die Exponenten variieren im Bereich von
etwa
. Viele reale Netze zeigen zwar
ein skalenfreies Verhalten, aber die Exponenten variieren im Bereich von
etwa 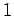 bis
bis 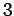 (siehe Tab. 1.1).
(siehe Tab. 1.1).



Nächste Seite: Das Modell von Dorogovtsev,
Aufwärts: Skalenfreie Netzwerke
Vorherige Seite: Skalenfreie Netzwerke
Inhalt
Autor:Lutz-Ingo Mielsch